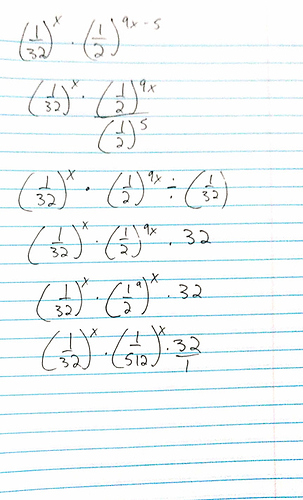0<n<=1/6
clearly n cannot be negative. multiply by n on both sides then divide by 6 on both sides.
I don't get it
Like yeah I get this but why am I not just finding the set of numbers where n is greater than or equal to 6
1/(6/36) definitely makes in the inequality true
ya but if you pick a number larger than 6/36 aka 1/6 for n, e.g., 1, the inequality's not satisfied
algebraically u just wanna multiply both sides by n and divide both sides by 6, which gives you
1/6 >= n
but then you also want to think about what makes the original inequality not work, e.g., n <= 0
therefore 0 < n <= 1/6
Yeah my brain stops working after I've been studying for like 3 hours
@electrowizard help 
Not with how to solve the question, but to explain why my brain found my answer instead of the correct one
you correctly found the cutoff point 6/36=1/6,but you have the direction wrong.
the correct answer is n<=6/36 and also n is positive so 0 < n <=1/6
dividing by a positive number changes the direction of <, > because dividing by bigger numbers get you smaller numbers. what you did was basically 1/(1/n) >= 1/6, which is incorrect because you need to flip the direction of the inequality if you do that. you would also need to consider the case where 1/n is negative.
for example, just consider the question
1/x >= 1/6.
clearly x=6 works.
x = 7 doesnt work because 1/7 < 1/6.
x = 5 works because 1/5 > 1/6.
x = -1 doesnt work because that makes 1/x go negative.
so 0 < x <= 6.
for the question its 1/x >= 1/(6/36) like you thought.
I feel like this shouldn't have been in the challenge problems section. I tend to overthink anything in the challenge problems section.
if you are familiar with the graph of 1/x it also makes the behavior of the solution set pretty obvious.
There was a problem on telescoping that was similar
Is this really prealgebra stuff? Am I really doing stuff that 5th graders do?
To become the master, you must first be a student
more like 7th grader unless nerd but yea
I passed this with an A in middle school I guess it just wasn't as rigorous
Not that that is a rigorous problem but some of the other ones