Stats/Math Problems and Riddles #2

General
1

I was going through some problems, thought I'd post some of the problems which the answers don't require a very mathy solution:

How can you generate a random number between 1 - 7 with only a die?

How can you get a fair coin toss if someone hands you a coin that is weighted to come up heads more often than tails?

A certain couple tells you that they have two children, at least one of which is a girl. What is the probability that they have two girls?

You have a group of couples that decide to have children until they have their first girl, after which they stop having children. What is the expected gender ratio of the children that are born? What is the expected number of children each couple will have?

2

fuck if i know

3

number 4 is the only interesting question the rest are trivial/dumb

so assuming 50% of getting boy/girl

if they get a girl, stop immediately

chance to get 1 boy: 50% for a boy, 50% for a girl

chance to get 2 consecutive boys: 50% * 50% = 25% for 2 boys, 75% for at least 1 girl

chance to get 3 consecutive boys: 12.5% for 3 boys, 87.5% for at least 1 girl

4 consec boys: 6.25%, 93.75% for at least 1 girl

etc.

so a couple can go on an unlimited streak of boys, but they can't go on an unlimited streak of girls (since it ends on the first one)

50% for 1 boy
25% for 2 boys (the percentage gets divided by 2, while number of boys gets multiplied by 2)
12.5% for 3 boys (percentage gets divided by 4 (from the start), while number of boys gets multiplied by 4

so the function is f(x) = 50% / x i think? but then im not sure how u solve it, in like, finding estimate number of average X if u rand it 1000 times or something

4

i think ur supposed to use that

lim something somethign thingy
x->ifninity

5

I don't think any are trivial. #1 you prob can't even solve if you don't know binary.

#2 I got completely wrong

If you think 1-3 are trivial I'm surprised you don't think #4 is equally trivial because if you play out the numbers you'll get to your answer rather easily assuming an equal probability exists for getting either a boy or girl.

6

for 1 dont you just ... throw the die? i dont get it?

for 2 how is it a math question? isnt it like a trick question, one of those "100 bets you'll never lose at a bar !!" things?

and for 3 its jsut 50%

7

lim

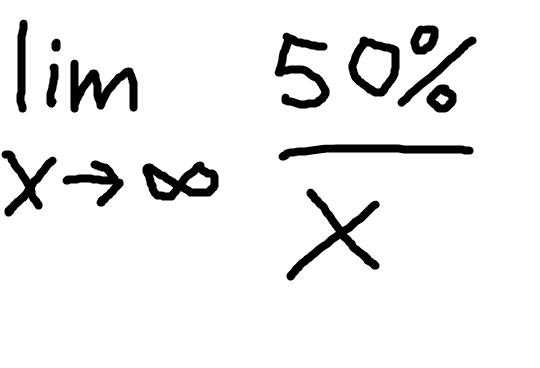
@iaafr is there a way to solve this or is this the answer?

8

If you have a 6 sided die, how do you throw the die in such a way that you can roll a number between 1-7 with equal probability?

Like throwing the die by itself has equal chance to land 1-6 but you need to find a way to throw it that you can count to 1-7

9

Lmao you got them all wrong. The coin one isn't a trick question at all.

None of these are trick questions and it isn't 1/2 for #3

10

i thought 1 and 7 exlucded. ok if they're included then:

2 extra numbers than the usual 6. so 33% increase. u can calcualte it with a die throw

2 numbers, one higher, one lower. 50/50, u can calcualte with a die throw

so u do this:

throw the die. if its 1, 2, 3, 4 => throw it again, and whatever u throw, thats the number. from 2 to 6.

if u roll 5 or 6, then throw again

if u roll 1, 2, or 3 => ur ending number is 1

if u roll 4, 5, 6 => ur ending number is 7

11

For #1 you need to find a system of throwing the die that let's you go up to 1-7, and I already hinted it requires you to know how to count in binary.

#2 say you have a coin that flips heads 9/10 times and tails 1/10 times, or some other value like 67/70 heads vs 3/70 tails, how do you flip the coin in such a way that the result is a 'fair' 50/50 between two players?

#3 it's not 1/2 lol, my hint is that you don't know if the first or second kid is a girl, so you need to imagine every possible scenario and pick from the ones which the question narrows down for you and then calculate the probability

#4 if you had 1000 couples and they had kids, try to imagine how it would play out and what the distribution might look like

12

well thats different. i was assuming a real-life scenario where some guy hands u a coin and u dont know how much is one side heavier than the other

and for number 3 its very obviously 50/50 lol

13

the image you posted is a trivial limit of the function 0.5/x as x goes towards infinity and it clearly = 0

unlikely this limit is involved in any solution

14

Based on the system you created, does each number have an equal chance of occurring like in the situation with the 1-6 die?

15

yea i think so

how is the answer to 3 not 50/50

there are 2 possibilites: girl/boy and girl/girl, lol

16

i dont even consider 3 a well formed question

looked up the answer to 2 and its pretty clever tho

17

wait i forgot how dies work. they count from 1-6. i thought they count from 2-6 i forgot they have the 1 oops

18

nvm

19

How many times can you roll the die?

20

For #1 just use a d7 die from D&D. Otherwise just have each number on the die represent a bit positions 1 2 3, and 4 5 6 also correspond to 1 2 3. Then roll it 3 times?